“温差能发电装置的原理及升压稳压模块设计”版本间的差异
来自iCenter Wiki
(以“== 温差能发电的基础原理——热电效应 == 温差能发电是一个直接将温度差所产生的能量转化为电能的过程。 具体来说,温差...”为内容创建页面) |
|||
| 第4行: | 第4行: | ||
=== 塞贝克效应(Seebeck Effect) === | === 塞贝克效应(Seebeck Effect) === | ||
| + | |||
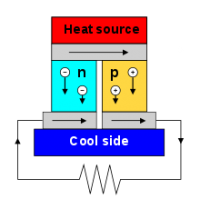
| + | [[文件:SeebeckEffect.png|200px|thumb|塞贝克效应:温差产生电流]] | ||
半导体在不同的温度下具有不同的载流子密度,当单一半导体两端具有温度差时,载子会扩散以消除密度的差异,因而造成电动势。 | 半导体在不同的温度下具有不同的载流子密度,当单一半导体两端具有温度差时,载子会扩散以消除密度的差异,因而造成电动势。 | ||
| 第10行: | 第12行: | ||
由塞贝克效应产生的电压可以表示成: | 由塞贝克效应产生的电压可以表示成: | ||
| − | |||
| − | |||
''S''<sub>A</sub>和''S''<sub>B</sub>是金属A和B的塞贝克系数,''T''<sub>1</sub>和''T''<sub>2</sub>是两块金属结合处的温度。塞贝克系数取决于温度和材料的分子结构。如果塞贝克系数在实验的温度范围内接近常数,以上方程可以近似成: | ''S''<sub>A</sub>和''S''<sub>B</sub>是金属A和B的塞贝克系数,''T''<sub>1</sub>和''T''<sub>2</sub>是两块金属结合处的温度。塞贝克系数取决于温度和材料的分子结构。如果塞贝克系数在实验的温度范围内接近常数,以上方程可以近似成: | ||
| − | |||
| − | |||
=== 帕尔帖效应(Peltier Effect) === | === 帕尔帖效应(Peltier Effect) === | ||
| + | |||
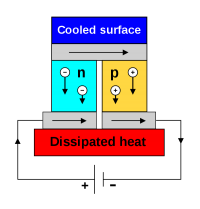
| + | [[文件:PeltierEffect.png|200px|thumb|帕尔贴效应:电流产生温差]] | ||
帕尔帖效应即為塞贝克效应的反效应,即当在两种金属回路中加入电源产生电势后,不同的金属接触点会有一个温差。 | 帕尔帖效应即為塞贝克效应的反效应,即当在两种金属回路中加入电源产生电势后,不同的金属接触点会有一个温差。 | ||
2018年12月4日 (二) 14:40的版本
温差能发电的基础原理——热电效应
温差能发电是一个直接将温度差所产生的能量转化为电能的过程。 具体来说,温差使导体(或半导体)的不同端产生物理性质差异(如平均自由程、载流子密度),进而产生恒定的电流和温差生电动势。
塞贝克效应(Seebeck Effect)
半导体在不同的温度下具有不同的载流子密度,当单一半导体两端具有温度差时,载子会扩散以消除密度的差异,因而造成电动势。
金属的赛贝克效应由电子的平均自由程来决定。 若平均自由程随温度上升,则热端的自由电子有较高的机会向冷端移动,此时的塞贝克系数为负值。 反过来说,若电子的平均自由程随温度上升而下降,则冷端的自由电子有较高的机会流向热端,塞贝克系数为正值。
由塞贝克效应产生的电压可以表示成:
SA和SB是金属A和B的塞贝克系数,T1和T2是两块金属结合处的温度。塞贝克系数取决于温度和材料的分子结构。如果塞贝克系数在实验的温度范围内接近常数,以上方程可以近似成:
帕尔帖效应(Peltier Effect)
帕尔帖效应即為塞贝克效应的反效应,即当在两种金属回路中加入电源产生电势后,不同的金属接触点会有一个温差。
Reference
- Thermoelectric Effect - Wikipedia: https://en.wikipedia.org/wiki/Thermoelectric_effect